Principle stresses in beams

Any beam in structure subjected to lateral loading; due to which bending and shear forces are developed in beam. Due to these forces bending and shear stresses are developed in beam.
Consider a beam of length ‘L’ is subjected to lateral load W/L as shown in fig. 9.a.
Take cross section of beam (section X-X)
b = breadth of beam;
d = depth of beam;
N.A. = Neutral axis;
AB = any fiber in beam;
y = dist. of fiber AB form N.A.;
Now,
σ_b= Bending stress in beam;
By flexural formula,


M = BM at sec. X-X;
I = Moment of inertia about N.A.;
y= dist. of fiber AB form N.A.;
Now,
q= Shear stress at fiber AB

Where,
q= Shear stress at fiber AB;
f = Shear force at X-X section;
A= Shaded area;
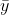= Dist. of shaded area from N.A.;
b= Width of AB;
I = Moment of inertia about N.A.