S.F & B.M. diagrams for beams subjected to uniformly distributed load (U. D. L.)
The process for SFD and BMD for uniformly distributed load is same as mentioned in SFD and BMD for point load but in this type we consider UDL instead of point load.
Draw SFD and BMD for simply supported beam having length 'L' and subjected to load 'W/L' as shown in fig.

Solution:
Step 1: Calculate support reactions
Put this value in Eq. 1
Step 2: Calculate Shear forces
1) Shear force just left of point A2) Shear force at just right of A
Only reaction due to A support is present in left side of section X-X and just right of point "A". And this reaction is upward. Upward forces at left of section are consider +ve. Therefor
3)Shear force at just left of B

There are two forces present in left side of sections X-X and just left side of point "B".
1. Reaction due to support A =
2. Force due to UDL =
Support reaction is +ve because by sign conventions; upward forces at left side of section X-X are taken as +ve.
Force due to UDL is -ve because by sign conventions; downward forces at left side of section X-X are taken as -ve. Therefore,
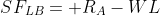



4)Shear force at just right of B1. Reaction due to support A =
2. Force due to UDL =
Support reaction is +ve because by sign conventions; upward forces at left side of section X-X are taken as +ve.
Force due to UDL is -ve because by sign conventions; downward forces at left side of section X-X are taken as -ve. Therefore,

There are three forces present in left side of sections X-X and just right side of point "B".
1. Reaction due to support A =
2. Force due to UDL =
3. Reaction due to support B =
Support reactions RA and RB are +ve because by sign conventions; upward forces at left side of section X-X are taken as +ve.
Force due to UDL is -ve because by sign conventions; downward forces at left side of section X-X are taken as -ve. Therefore,
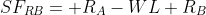



All these SF calculated summarized as below,




1. Reaction due to support A =
2. Force due to UDL =
3. Reaction due to support B =
Support reactions RA and RB are +ve because by sign conventions; upward forces at left side of section X-X are taken as +ve.
Force due to UDL is -ve because by sign conventions; downward forces at left side of section X-X are taken as -ve. Therefore,
All these SF calculated summarized as below,
Step 3: Draw SFD
Now, SFD is drawn as below(Note: SFD must be drawn below the beam)
Step 4: Calculate bending moments
1) Bending moment at point A
There is no any force in left side of point A. Therefore,

2) Bending moment at point CBefore calculating bending moment at B; we have calculate bending moment at zero shear which is called as point of contra shear. Because at point of zero shear bending moment is maximum.
This point of zero shear named as point C.
This point of zero shear named as point C.

Assume distance between point of zero shear and support A is X as shown in fig. Taking summation of total shear forces at point C equals to zero. Consider left side of point C.

There are two forces presents in left side of section X-X and left of point C.
1. Reaction due to support A =
2. Force due to UDL =
Support reaction RA is +ve because by sign conventions; upward forces at left side of section X-X are taken as +ve.
Force due to UDL is -ve because by sign conventions; downward forces at left side of section X-X are taken as -ve. Therefore,

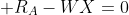





Now, calculate bending moment at C.

There are two moments are acting at left side of point C.
1. Moment due to support A = Force X dist. =)
2. Moment due to UDL = Force X dist. =)
Support reaction RA is +ve because by sign conventions; clock wise moment at left side of section X-X are taken as +ve.
Force due to UDL is -ve because by sign conventions; anti clock wise moment at left side of section X-X are taken as -ve. Therefore,
-\left (\frac{WL}{2}\times \frac{L}{4} \right ))
-\left ( \frac{WL^{2}}{8} \right ))
-\left ( \frac{WL^{2}}{8} \right ))
-\left ( \frac{WL^{2}}{8} \right ))
)
)
3) Bending moment at point B

There are two moments are acting at left side of point B and section X-X.
1. Moment due to support A = Force X dist. =)
2. Moment due to UDL = Force X dist. =)
Support reaction RA is +ve because by sign conventions; clock wise moment at left side of section X-X are taken as +ve.
Force of RA is and acting at distance L.
and acting at distance L.
Moment due to UDL is -ve because by sign conventions; anti clock wise moment at left side of section X-X are taken as -ve.
Force of UDL is WL and acting at distance L/2.
Therefore,
-\left ( WL\times \frac{L}{2} \right ))
-\left ( \frac{WL^{2}}{2} \right ))

All moments are summarized as below,

)

(Note: SFD must be drawn below the beam and BMD must be drawn below the SFD.)
1. Reaction due to support A =
2. Force due to UDL =
Support reaction RA is +ve because by sign conventions; upward forces at left side of section X-X are taken as +ve.
Force due to UDL is -ve because by sign conventions; downward forces at left side of section X-X are taken as -ve. Therefore,
Now, calculate bending moment at C.

There are two moments are acting at left side of point C.
1. Moment due to support A = Force X dist. =
2. Moment due to UDL = Force X dist. =
Support reaction RA is +ve because by sign conventions; clock wise moment at left side of section X-X are taken as +ve.
Force due to UDL is -ve because by sign conventions; anti clock wise moment at left side of section X-X are taken as -ve. Therefore,
3) Bending moment at point B

There are two moments are acting at left side of point B and section X-X.
1. Moment due to support A = Force X dist. =
2. Moment due to UDL = Force X dist. =
Support reaction RA is +ve because by sign conventions; clock wise moment at left side of section X-X are taken as +ve.
Force of RA is
Moment due to UDL is -ve because by sign conventions; anti clock wise moment at left side of section X-X are taken as -ve.
Force of UDL is WL and acting at distance L/2.
Therefore,
All moments are summarized as below,
Step 5: Draw BMD
Now, BMD is drawn as below(Note: SFD must be drawn below the beam and BMD must be drawn below the SFD.)





















0 comments